Témavezető: Dr. Kertész János

Tanszék/Intézet: Elméleti Fizika Tanszék / Fizika Intézet

 

Kommunikációs dinamika modellezése

A kutatási téma néhány soros bemutatása

Kutatási területem az emberi viselkedés infokommunikációs adatok alapján történő elemzése és modellezése. Munkám során egyrészt méréseket végzek telekommunikációs idősorokon, másrészt matematikai modelleket keresek a jelenségek leírására. A modelleket numerikus módszerekkel tanulmányozom, valamint analitikusan is próbálom azokat megoldani.

A kutatóhely rövid bemutatása

Kutatásaimat az Elméleti Fizika Tanszéken végzem, együttműködve a finn Aalto Egyetem kutatóival, akiknek hozzáférésük van egy nagyméretű infokommunikációs adatsorhoz. Nyári gyakorlatomat náluk, az Aalto Egyetemen töltöttem.

A kutatás történetének, tágabb kontextusának bemutatása

A humán dinamika tárgya az emberi viselkedés tanulmányozása, elsősorban statisztikus fizikában is használt módszerek segítségével. A terület gyors fejlődését a nagyméretű elektronikus adatbázisok megjelenése és hozzáférhetősége indította el (pl. email [1] és telefonhívási adatbázisok [2]). Az egyik legfontosabb kérdés az emberi tevékenységek időzítése. Megállapították, hogy az események között eltelt idő vagy a várakozási idők lecsengése sok esetben hatványfüggvénnyel közelíthető. Az első eredmények között szerepelt, hogy a kitevő email-kommunikáció esetén 1 [1], hagyományos postai levelezés esetén pedig 3/2 [3]. Az Aalto egyetem kutatóinak mérései alapján a telefonálás esetében is hatványlecsengésű (megfelelő levágásokkal) az események közötti idő eloszlása, valamint az autokorrelációs függvény is [4].

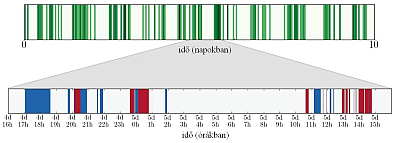
1. ábra Emberi tevékenységek tipikus időzítése. Felső ábra: hívási aktivitás napi skálán, sötétebb árnyalat nagyobb hívássűrűséget jelent. Alsó ábra: egy nap kinagyított képe, az indított hívások színe kék, a fogadottaké bordó.

A terület virágzását 2005 óta éli, amikor Barabási Albert egy egyszerű sorbanállási modellt [5] mutatott be, ami magyarázza az email kommunikációban megjelenő hatványfüggvény lecsengésű várakozási időt.
2008-ban egy kaszkád inhomogén Poisson-folyamatra épülő magyarázat is született az email kommunikációban megjelenő hosszú farkú eloszlásokra [6]. Azóta a kutatók megosztottak, egyesek szerint az események közötti idők széles eloszlása csupán az életben megfigyelhető ciklikus jelenségeknek a következményei, mások szerint emellett jelen van valamilyen belső, hosszú memóriájú folyamat is.
 

A kutatás célja, a megválaszolandó kérdések

Mérések:
Az irodalomban található mérések jelentős részében a teljes adatsorra vonatkozó átlagok szerepek. Egyik célom, hogy ezzel a trenddel szemben, az egyének oldaláról is megvizsgáljam az idősorokat. A vizsgálatok eredménye megerősítheti, vagy elvetheti az átlagolás jogosságát. Ehhez kapcsolódó kérdés, hogy a mobiltelefon-felhasználók nagyjából ugyanúgy viselkednek-e, vagy jelentős különbségek vannak közöttük (a hívások átlagos gyakoriságától eltekintve). Ha ez utóbbi áll fenn, akkor kérdéses, hogy milyen kategóriák jelennek meg. Arra is keresem a választ, hogy jogos-e statikusan kezelni a felhasználókat, vagy fél éves skálán már kimutathatóan változhatnak a telefonálási szokások.

Modellezés:
Másik célom, hogy a megfigyelt jelenségeket reprodukáló modelleket találjak, és ezek egyszerűsített változatait megoldjam. A Barabási-féle sorbanállási modellben például nem lehet események közötti időket definiálni, csak várakozási időket (ami az email érkezése és a válasz küldése közt eltelt idő), és emiatt az autokorrelációs függvény is nehezen értelmezhető. Célom volt tehát olyan modellt keresni, amiben definiálható az események közötti idő és az autokorrelációs függvény, valamint amiben ezen mennyiségek hatványlecsengést nyújtanak (a méréseknek megfelelően hangolható kitevőkkel).
Szintén szükséges megvizsgálni a kaszkád inhomogén Poisson-folyamat alkalmazhatóságát a telefonálási adatsor modellezésében.

Módszerek

Mérések:
Az Aalto egyetem adatsorának egy 70 fős, csak az események közötti időket tartalmazó kivonatát tanulmányoztam. Az egyes felhasználókhoz tartozóan sokféle mennyiséget és függvényt meghatároztam, többnyire hisztogramok segítségével. A legfontosabbak az események közötti idő eloszlása, az autokorrelációs függvény, a napi ritmus (hívási ráta változása a nap folyamán), az egyes napokon indított hívások száma, valamint egy a finn kutatócsoport által bevezetett mennyiség a korrelációk mérésére [4].

 

Modellezés:

Sorbanállási modell: Egy prioritás alapján rendezett, dinamikusan változó listán alapuló modellt tanulmányoztam, ami a Barabási modell egyfajta általánosítása. Az alapvető különbség az, hogy az általam vizsgált modellben a végrehajtott cselekvés nem kerül ki a listából. A modellnek 3 paramétere van: a lista hossza, a listában szereplő telefonálási tevékenységek száma, és egy, a listából történő választást jellemző paraméter. Numerikus módszerekkel meghatároztam a modell események közötti idő eloszlását és  autokorrelációs függvényét a bemenő paraméterek különböző értékeire. Az eredményeket végesméret-skálázás segítségével elemeztem. A numerikus eredmények alátámasztására néhány esetben Monte Carlo szimulációt is végeztem. Ezek mellett a modellt analitikusan is próbáltam kezelni.

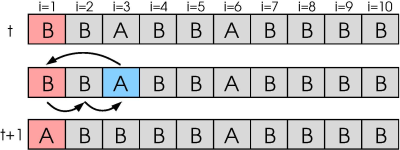
2. ábra A végrehajtandó tevékenységek (A: telefonálás, B: egyéb) egy listában helyezkednek el. Minden lépésben kiválasztjuk a lista egy véletlen elemét, úgy hogy az elejéből nagyobb valószínűséggel választunk. A kiválasztott tevékenység a lista elejére ugrik. Ez a folyamat egy Markov-láncot definiál.

Az elemzés során logaritmikus generátorfüggvényeket (Laplace transzformáltakat), az aszimptotikus viselkedés tanulmányozására Tauber-ill. Abel tételeket [7] használtam. Az események közötti idők eloszlásának meghatározásának problémáját sikerült visszavezetnem egy parciális differenciálegyenlet megoldására.

Inhomogén Poisson-folyamat:
Szimulációkat és analitikus számolásokat végeztem a folyamat események közötti idő eloszlására és az autokorrelációs függvényére. Az analitikus formulákat néhány egyszerű esetben értékeltem ki (négyszögjel és szinuszos alakú rátafüggvényekre).

Eddigi eredmények

Mérések: Események közötti idő eloszlása: A különböző felhasználókra hasonló alakú, a hatványfüggvény szakaszon kívül két csúcs is megfigyelhető (3.ábra): az egyik rövid időknél, a másik pedig 12 óra és 1 nap között, pontos helye függ a felhasználó aktivitásától. Ez utóbbi megjelenését az inhomogén Poisson-folyamat tudja magyarázni (éjszakai inaktivitás). A [6] cikkben bevezetett kaszkád folyamat hozzáadása azt jelenti, hogy a hívások egy magasabb rátájú Poisson-folyamatot indukálnak. Ezzel a kezdeti csúcs magyarázható, azonban a hatványfüggvényszerű szakasz nem. Hasonló hiányosság jelentkezik az autokorrelációs függvény esetében is.

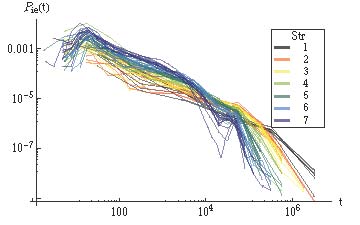3. ábra Események közötti idő eloszlása. A színek a felhasználó aktivitását jelölik.

 

Autokorrelációs függvény: A hosszú távú korrelációk az inhomogén Poisson-folyamat jóslatának megfelelően napi periodicitást mutatnak. A függvény alakja különbözik az egyes emberekre, a mért napi ritmussal összehasonlítva 4 kategóriába tudtam sorolni a felhasználókat, azonban a kategóriák közötti határ nem éles (a 4.ábrán nem ez, hanem az aktivitás szerinti csoportosítás látható). Rövid távú korrelációknál szintén eltérést tapasztaltam az inhomogén Poisson-folyamattól (5. ábra). A kezdeti csúcs lecsengése sok esetben hatványfüggvénnyel közelíthető, amit a [6].cikkben közölt kaszkád-konstrukció nem tud reprodukálni.

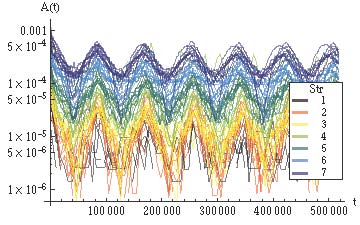4. ábra Autokorrelációs függvény. A színek a felhasználó aktivitását jelölik

 

Hívások napi mennyisége:
Meglepő módon a felhasználók kevesebb, mint felénél mutatkozik jól látható heti és havi ritmus.
Fél éves skálán a felhasználók több mint negyede változtatta telefonálási aktivitását (az esetek felében nullára, ami valószínűleg utazásokhoz kapcsolódik).
 

 

5. ábra Autokorrelációs függvény (felső vonal) eltérése rövid időkre az inhomogén Poisson folyamattól 3 felhasználó esetén, a tengelyek logaritmikusak. A belső grafikonon a:függőleges tengely lineáris, a vízszintes pedig logaritmikus. Az idő másodperces egységekben adott.

 

Konklúzió: az inhomogén Poisson-folyamat a kb. 3 óránál későbbi időkre kvalitatívan jó eredményt ad. Méréseim alapján a [6] cikkben közölt kaszkád folyamat nem tudja kielégítően magyarázni a rövidtávú viselkedést. Egy lehetséges általánosítását adná a modellnek, ha a kaszkád folyamatnak nem egy magasabb rátájú Poisson-folyamatot, hanem egy sorbanállási modellt választanánk.

 

Modell:
Jelentős eredményeket a sorbanállási modellben értem el. Beláttam, hogy a modell autokorrelációs függvénye nem függ a listában szereplő tevékenységek számától. A numerikus eredmények vizsgálata során észrevettem, hogy a különböző listahosszak mellett mért autokorrelációs függvények hatványlecsengésűek, valamint összeskálázhatók (fedésbe hozhatók egymással). Az exponens értékét végesméret-skálázás segítségével meghatároztam a modell bemenő paramétereinek függvényében. Numerikus számításaim alapján az események közötti idők eloszlása hatványlecsengésű, és megfogalmaztam egy sejtést a kitevő értékére a modell paramétereinek függvényében. A két kitevő (numerikusan) teljesít egy skálatörvényt, mely szerint a kitevők összege 2. Ezt a skálatörvényt analitikusan bizonyítottam, és kiterjesztettem a modellek szélesebb családjára: minden olyan pontfolyamatra, amit független, hatványeloszlású események közötti idők definiálnak.
Végezetül a modell egy paraméterértékére sikerült analitikusan meghatároznom az események közötti idő eloszlásának lecsengését, amiből a skálatörvénnyel már számolható az autokorrelációs függvény.
 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája
A skálatörvényt és a sorbanállási modellel kapcsolatban elért eredményeket szeretnénk publikálni, már belekezdtünk a cikk megírásába.
 

Linkgyűjtemény
Humán dinamika, rövid összefoglaló a Wikipedián (angolul)
Poisson-folyamat a Wikipedián (angolul)
Aalto egyetem kutatócsoportjának honlapja

Hivatkozások listája
[1] J.-P. Eckmann, E. Moses, D. Sergi, Proc. Natl Acd. Sci. USA 101, 14333 (2004).
[2] W. Aiello, F. Chung and L. Lu (2000) Proceedings of the 32nd ACM Symposium on the
Theory of Computing (ACM, New York), pp. 171-180.
[3] J. G. Oliveira and A.-L. Barabási, Nature (London) 437, 1251 (2005).
[4] M. Karsai, K. Kaski, A.-L. Barabási, J. Kertész (publikálás alatt)
[5] A.-L. Barabási, Nature (London) 435, 207 (2005)
[6] R.D. Malmgren, D.B. Stouffer, A.E. Motter, L.A.N. Amaral, Proc. Nat. Acad. Sci. 105, 18153 (2008).
[7] W. Feller, An Introduction to Probability Theory and its Applications 2nd ed. Vol. 2., Wiley
India Pvt. Ltd. (2008).