|
BMe TTK Kutatói pályázat |

|
Témavezető: Dr. Simon Ferenc
Tanszék/Intézet: Fizika Tanszék
Szilícium napelem minták kristályossági fokának vizsgálata Raman-spektroszkópiai módszerekkel
A kutatási téma néhány soros bemutatása
A mérések célja a napelemet alkotó szilícium szilárdtest réteg kémiai összetételének és morfológiájának meghatározása, a szilícium rezgési spektroszkópiájának mérésével. Az így kapott eredmények a napelemek hatásfokának fejlesztése szempontjából lényegesek.
A kutatóhely rövid bemutatása
2011 nyarán, a Semilab Zrt. félvezető kutató laboratóriumában végeztem ipari célú kutató munkát, melynek célja vékony-film (µc-Si) napelemek optikai módszerrel történő karakterizálása a Si fázisarányának meghatározásával.
Kutatómunkámat az optikai osztálynál végeztem, melynek lényege a következő: Egy napelem gyár által küldött mintasorozatban kellett meghatároznom a mikrokristályos Szilícium (µc-Si ) és az amorf Szilícium( a-Si) fázisok arányát Raman-szórással. Így a napelemek hatásfokát befolyásoló morfológiai és anyagi jellemzők ismeretéhez juthatunk el.
A hosszú távú cél egy olyan Raman-szóráson alapuló optikai eljárás kidolgozás, mely rövid idő alatt megbízható információt szolgáltat a fent említett fázisarányról.
A kutatás történetének, tágabb kontextusának bemutatása
Napjainkban egyre fontosabb szerep jut a roncsolásmentes mérési módszerek alkalmazásának, ezek egyik legfontosabb célja az ipari technológia folyamatainak irányítása, a termékek minőségellenőrzése és minőségbiztosítása.
A számtalan optikai (látható-fény, IR és UV) roncsolásmentes mérési módszerek egyike a Raman-spektroszkópia melyet a következő pontban ismertetek.
A vékonyréteg napelemek ipari karakterizálásának szempontjából a Raman-spektroszkópia különösen hasznos a következő 3 ok miatt:
1- A mérés rendkívül rövid idő alatt elvégezhető (0,7-5 másodperc / minta), mely lehetőséget teremt a valós idejű mérések végrehajtásához, ez nyilvánvalóan iparilag fontos szempont.
2- A Raman-spektroszkópiában szilícium napelemek mérésére használt gerjesztés behatolási mélysége a mintában mikrométer nagyságrendű, ami pontosan egy vékonyréteg napelem karakterisztikus vastagsága, így a mérés szempontjából az összes gerjesztő foton szenvedhet Raman-szórást, és a napelem minden kémiai rétegéről ad információt.
3- A szilícium rendelkezik egy karakterisztikus Raman-módussal 520 cm-1 Raman-shift érték körül, melynek nagysága és szélessége igen pontos és specifikus információt hordoz a szemcseméretről és a kristályosság mértékéről. E módus vizsgálata tehát ideális a fent ismertetett fontos karakterizálás szempontjából.

1. kép Egy µc-Si napelem cella transzmissziós elektronmikroszkópos keresztmetszete . A jobb oldali panel mutatja a struktúra szerkezetét sematikusan . A ZnO hordozón lévő amorf Szilícium egyenletesen szürke, ennek tetején látható a kúp alakú konglomerátumot (∆) alkotó mikrokristályos Szilícium granulák (δ). [Dorz 2003]
A Raman-spektrum kiértékelése során kiszámolható a kristályos fázisnak a térfogat hányadosa. Ezt a mennyiséget nevezzük Raman kristályossági faktornak:
![]() [1]
[1]
ahol Vc a kristályos fázis térfogata és Vexp a teljes besugárzott térfogat.
A kutatás célja, a megválaszolandó kérdések
A fosszilis energiahordozók véges mennyisége, és felhasználása által okozott környezeti károk miatt, a mai modern technológiában egyre jobban előtérbe kerül a megújuló energiahordozók szerepe, köztük is kiemelkedő fontosságú a napenergia.
A napelem egyszerűsített működési elve a következő: a napelem cellában lévő félvezetőben elnyelt foton elektron-lyuk párokat kelt (fotoeffektus). A félvezetőre kontaktusokat helyezve ezek a töltéshordozók az előfeszített tér hatására elmozdulnak az elektródák irányába, melyeket elérve hasznos árammá alakul.
Adódik a kérdés: mitől függ, hogy a töltéshordozó eléri-e az elektródát? Ha az elektron-lyuk párok adott része rekombinálódik mielőtt elérnék az elektródát, akkor ez nem hasznosítható az áram szempontjából. A napelem hatásfokát jellemző lényeges paraméter tehát a fény által keltett töltéshordozók szabad úthossza (a rekombinációig megtett átlagos hossz). Fontos tehát olyan félvezetőanyagot választani, amiben a szabad úthossz minél nagyobb.
A Si alapú napelemek felhasználásával kapcsolatosan a következő probléma merül fel. A Si egykristályból (c-Si) álló napelemben közismert, hogy a szabad úthossza nagy, ám ilyen napelemek gyártás meglehetősen drága és időigényes a mai technológiával.
Ha a Si amorfos fázisban (a-Si) fordul elő a napelemben, akkor ennek a szabad úthossza jóval kisebb, így az ilyen szilíciumra alapozott napelem hatásfoka jóval rosszabb az c-Si napeleménél, viszont ennek előállítása jóval olcsóbb is. Így adódik a kérdés, azaz előállítható-e olyan, szilíciumból készült napelem melynek hatásfoka elfogadható, és gazdaságilag is előnyös. A kérdésre a válasz igen: amennyiben a napelem cella félvezetőanyaga tartalmaz egyszerre mikrokristályos Szilíciumot ( µc-Si ) és amorf Szilíciumot is (a-Si), így hatásfoka széles tartományban hangolható a célnak megfelelően.
Módszerek
Elméleti bevezető:
A kristályos szerkezetek meghatározó tulajdonsága az ún. fonon: ez az
anyag atomjainak az egyensúlyi helyzet körül végzett kollektív rezgését
(azaz a normál rezgéseket, vagy normál módusokat) írja le. A rezgés
frekvenciája adott módusra állandó az anyagban, a különböző atomok rezgési
fázisa tér el.
Ennek matematikai alakja:
![]() [2]
[2]
ahol Qj egy
atom kitérése az egyensúlyi helyzetből (normál koordináta), Aj annak
amplitúdója és i a képzetes egység,q a hullámszám vektor .
A Raman-szórás klasszikus tárgyalása
Ismeretes, hogy ha egy dielektrikumot (vagy félvezetőt) elektromos térbe helyezünk, akkor lokálisan indukálódik egy dipólmomentum melynek nagysága gyenge elektromos tér esetén a térrel lineáris :
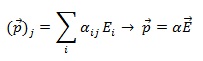 [3]
[3]
ahol α jelöli a polarizálhatósági tenzort (mátrix), itt jegyezzük meg, hogy ez egy molekula esetén függ az atomok távolságától .
A továbbiakban vegyünk egy egyszerű két atomos molekulát mely wj körfrekvenciával rezeg egyensúlyi helyzetéhez képest [2], és a térerősséget egy gerjesztő LASER elektromos térerő komponense adja:
![]() [4]
[4]
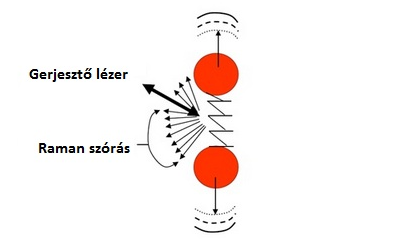
2.kép Rezgő dipólis kölcsönhatása a külső gerjesztő elektromos térrel.
mivel a polarizálhatóság függ az atomok távolságától, ezért a
polarizálhatósági tenzor sorbafejthető
,Qk normálkoordináták
szerint mátrixos
jelölésben ![]() [5]
[5]
ahol: αd
az ún. Raman tenzor,
αo A
Rayleigh tenzor
behelyettesítve [3]-ba [2],[4],[5] alakokat és felhasználva a koszinuszok
szorzatára vonatkozó addíciós tételt ![]() adódik:
adódik:
![]() [6]
[6]
tehát megjelent a gerjesztés és a sajátrezgés frekvenciáinak a különbségi
és összegi frekvenciával rezgő dipól tag!
adott frekvenciával rezgő dipól ugyanolyan frekvenciájú elektromágneses sugárzást bocsájt ki, melynek teljesítménye:
![]()
A [6] képletben szereplő első tag a Rayleigh-sugárzás, második két tag Raman-sugárzás ( Stokes és anti-Stokes). Általában a Rayleigh-sugárzás intenzitása 5-7 nagyságrenddel nagyobb, mint a Raman-szórás. A Raman-spektroszkópiában használt egység az ún. Raman-shift:
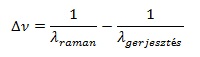
ahol λ a hullámhosszt jelöl. A Raman-eltolás mértékegysége az ún. hullámszám: cm-1
Egy sematikus Raman spektrumot ábrázol az alábbi kép:
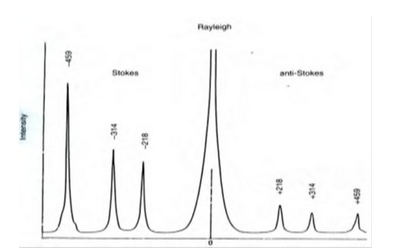
3. kép CCl4 Raman spektruma Vegyük
észre a 0cm-1 Raman shiftnél lévő igen intenzív Rayleigh
sugárzást és az ekörül
szimmetrikusan elhelyezkedő Stokes ill. Anti-Stokes Raman vonalakat, melyek csak intenzitásukban különböznek. [Kit Umbach]
Raman-kristályossági faktor
Korábban bevezettük a Raman-kristályossági faktor fogalmát
![]()
ahol Vexp =
Vc +
Va (Vc és
Va a
kristályos és amorf fázisok térfogata). Az ezekhez tartozó Raman-szórás
intenzitása arányos a térfogattal és a hatáskeresztmetszettel.
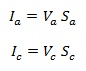
ahol Sa és Sc az adott fázishoz tartozó integrált hatáskeresztmetszet. Ezeket behelyettesítve [1] -be adódik:
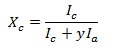
ahol y az Sc és Sa hányadosa. ennek értéke körül máig forognak viták: [Tsu 1982] y = 0,88,[Bustarret 1988] y= 0,5 ,[Dorz 2003] y= 1,7-1,8
annyi biztos, hogy y gerjesztő frekvencia és granulátum mért függvénye [Bustarret 1988].
Ezek kiküszöbölésére önkényesen y = 1 -nek választjuk. Ezt a választásunkat az indokolja, hogy a közvetlen célunk nem a valódi kristályossági hányados meghatározása, hanem egy olyan egzakt módszer kidolgozása melyben egy napelem hatásfokát befolyásoló tényező egyértelműen meghatározható egy mért eredményből (a valódi és a mért kristályossági faktor közt egyértelmű megfeleltetés van)
Kísérleti berendezés:
Gerjesztés:
A mérésekhez használt lézer, egy 532 nm-s (zöld) félvezető diódalézer.
Teljesítmény: változtatható (< 10mW a mintán)
Fénygyűjtés
Raman-spektroszkópia egyik legfontosabb eleme, hogy hogyan szabaduljunk
meg a Rayleigh-sugárzástól. A Rayleigh- sugárzás 5-7 nagyságrenddel
nagyobb, mint a Raman-sugárzás melynek detektálásához igen érzékeny
detektorok szükségesek (PMT, CCD), ez azt jelenti, hogy a
Rayleigh-sugárzás telítésbe vinné a detektort.
A berendezés elvi vázlatát a 4. képen mutatom.
|
|
|
|
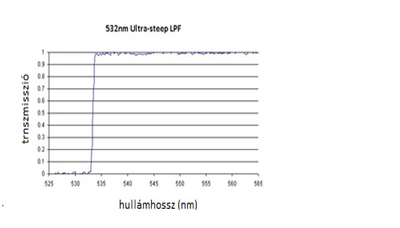
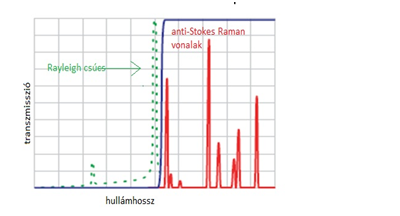
4.kép baloldal: fénygyűjtő berendezés sematikus rajza. Középen a long-pass szűrő transzmissziós görbéje, jobboldalon a szűrő hatása a spektrumon: kék transzmissziós görbe, a szaggatott zöld vonalakat a szűrő OD7 -el elnyomja
A mérési elrendezés felépítése a következő. A mintát gerjesztő lézer fénye egy 45° dőlésszögű tükrön fúrt lyukon keresztül esik a mintára. A minta egy gyűjtő objektív lencse fókuszában helyezkedik el, ami a mintáról minden irányban egyenletesen (izotrópan) szóródó Rayleigh és Raman fényt kollimálja (párhuzamosítja). Ezt a fényt a tükör a spektrográf felé továbbítja. A fény útjába egy ún. "long-pass" Raman-szűrőt helyezünk, ami a Rayleigh fényt igen hatékonyan (OD7 azaz 107-es elnyomás) kiszűri, viszont a Stokes-Raman vonalakat igen jól (a transzmisszió 98 %) átengedi.
Spektrográf
Ahhoz, hogy a Raman-jelet mérni tudjuk, szükség van a jel hullámhossz szerinti felbontására. A méréseknél használt spektrográf, egy optikai rács segítségével bontja fel a bejövő fényt a komponensek hullámhossza szerint (diszperzív felbontás).
A spektrográf elrendezése a következő:
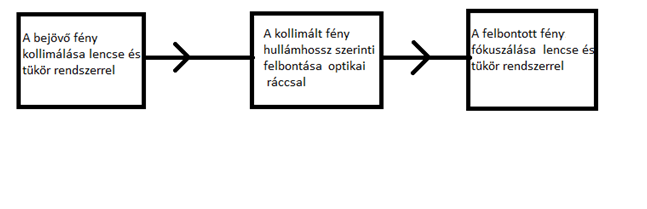
5. kép OSLO optikai tervező programban készült spektrográf sematikus felépítése, hullámhossz szerinti felbontást az "optical grating" (optikai rács), végzi, ezután
fókuszáló tükör minden hullámhosszat (spektrális komponenst) a CCD különböző pixel oszlopára fókuszál
Eddigi eredmények
Vékonyréteg napelem Raman-spektrum
A Raman-spektrum 3 spektrális komponensből áll, így illeszthetünk egy
Gauss görbét minden egyes "csúcsához".
• A keskeny csúcs, mely 520 cm-1 -nél látható, tartozik a kristályos
Szilícium (c-Si) TO módusához
(Transzverzális Optikai) ennek jellegzetes félértékszélessége 10±1 cm-1.
•
A közepesen széles csúcs, amely 510 cm-1 -nél látható, tartozik olyan
kristályos granulákhoz, melyek átmérője kisebb 10nm, vagy a Szilícium
ún. Wurzite fázisához (a [6] ábrán defektív kristályos fázis). Ennek
jellegzetes félérték szélessége 26±2 cm-1
•
A kiemelkedően széles csúcs 481 cm-1 nél az amorf Szilícium fázis (a-Si:H)
TO módusához tartozik,
ennek jellegzetes félértékszélessége 53±7 cm-1
µc-Si Napelem Raman spektrumát mutatja az alábbi ábra:
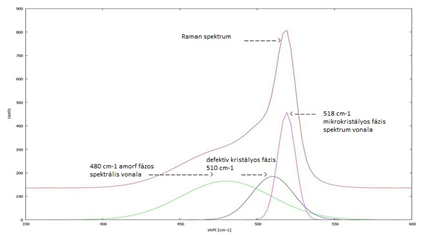
6.kép Piros: Vékonyréteg napelem jellegzetes Raman- spektruma, mely
3 spektrumkomponens összegeként áll elő (lila, zöld és kék)
a Raman kristályossági faktor meghatározásához az [5] összefüggést
használjuk mely y=1 helyettesítéssel a következő alakot veszi fel: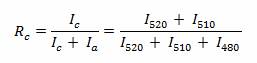
Ahol I520 , I510 , I480 a
megfelelő Gauss görbék alatti terület mértéke.
A következő mintasorozaton jól látható a spektrális különbségek a Raman
kristályossági faktor függvényében.
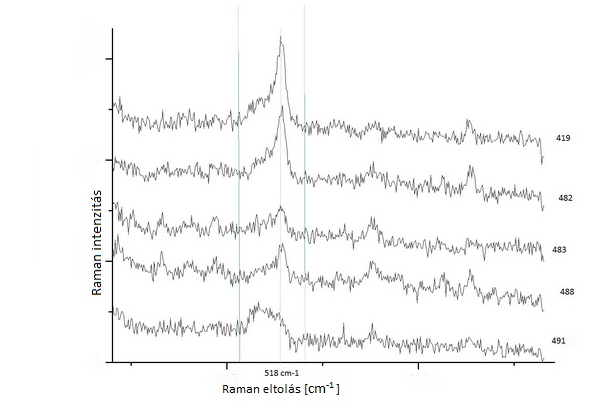
7.kép Különböző kristályossági faktorú minták Raman spektruma. A spektrumok melletti számok különböző minta sorszámot jelentenek
Az ábrán jól látható, hogyan alakul a Raman-spektrum a kristályossági faktor változásával.
A minták kristályossági faktorát a mért adatokból következtetve:
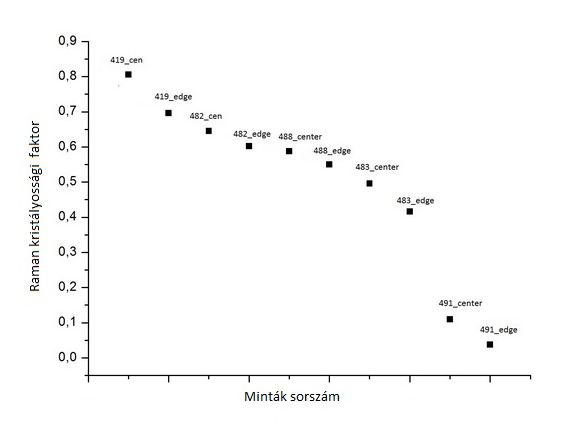
8.kép a 7. ábrán lévő napelem mintasor intrinsic réteg közepén és szélén mért Raman kristályossági faktor.
Megjegyezzük, hogy a kristályossági faktor a minta szélein átlagosan 10% -al kisebb, mint közepén
Egy Sunpreme napelemekből álló minta sorozaton mért spektrum és számított kristályossági együtthatót mutat az alábbi ábra.
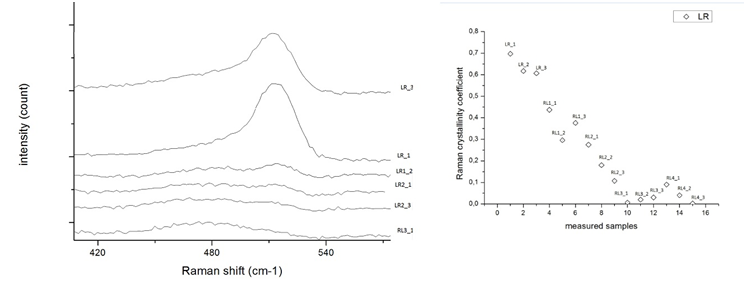
9. ábra baloldal: Sunpreme mintasorozat különböző spektrumok, és a mért kristályossági faktor
Összefoglalás
Tanulmányomban megmutattam a Raman-szórás klasszikus fizikai alapjait, majd ismertettem a vékonyréteg szilícium napelemeknél használt Raman kristályossági faktor fogalmát és hogy mi a kapcsolata a valódi kristályossági faktorral és egyes Raman-módusok intenzitásával.
Továbbá megmutattam, hogy milyen kísérleti berendezés szükséges egy látható-fény Raman-spektrum felvételéhez, illetve ismertettem spektrum kiértékelésének módszerét.
Végezetül az eddig elmondottakat megmutattam két szilícium napelem minta sorozaton.
Dolgozatom célja az volt, hogy megismertessem egy, a napelemek fejlesztésében és gyártásában alkalmazható analitikai módszer, mely Magyarországon elsőként a Semilab Zrt. fejlesztett ki ipari célokra, és ennek a fejlesztésnek részese lehettem szakmai gyakorlat keretében.
Konklúzió
A napelemek fejlesztésében és gyártásban igen fontos szerepe jut a Raman-spektroszkópiának. Ebben a tanulmányban megmutattam, hogyan lehet egy mikrokristályos szilícium napelem kémiai összetételéről quantitatív információkat meghatározni Raman-spektrum mérésével. Mindez igen érzékeny detektorok, optikai elemek alkalmazást és gondosan megtervezett optikai mérőberendezés összeállítást követel meg, mely az utóbbi két évtized technikai fejlődése az elektronika és optika területén tett lehetővé.
Saját publikációk, hivatkozások, linkgyűjtemény
Kit Umbach (képek forrása)
Corine Dorz [2003] Thin Film Microcrystalline Silicon Layers and Solar Cells: Microstructure and Electrical Performances doktori értekezés
Ian R. Lewis; Howell Edwards [2001]: Handbook of Raman Spectroscopy: From the Research Laboratory to the Process Line
Arvind Victor Shah [2010] Thin-film Silicon: Photovoltaics and Large-area Electronics